ปริมาณทางฟิสิกส์แบ่งออกได้เป็น 2 ประเภท
1. ปริมาณสเกลาร์ ( Scalar )
คือ ปริมาณที่จะมีแต่ขนาดเท่านั้น ไม่มีทิศทาง การคำนวณสามารถบวก ลบ คูณ หาร ได้ทั่ว ๆ ไป
ตัวอย่าง ปริมาณสเกลาร์ เช่น ระยะทาง ( Distance ) มวล ( Mass ) อัตราเร็ว ( Speed ) ความหนาแน่น ( Density )
2. ปริมาณเวกเตอร์ ( Vector )
คือ ปริมาณที่มีทั้งขนาด และทิศทาง การคำนวณจะใช้วิธีต่าง ๆ ที่แตกต่างจากการคำนวณทั่วไป
ตัวอย่าง ปริมาณเวกเตอร์ เช่น การกระจัด ( Displacement ) แรง ( Force ) ความเร็ว ( Velocity )
ความเร่ง ( Acceleration )
การรวมเวกเตอร์
คือ การบวกหรือลบกันของเวกเตอร์ตั้งแต่ 2 เวกเตอร์ขึ้นไป ผลลัพธ์ที่ได้เป็นปริมาณเวกเตอร์
เรียกว่า เวกเตอร์ลัพธ์ ( Resultant Vector )
มี 2 วิธีดังนี้
1) วิธีวาดรูป ( วิธีหัวต่อหาง )
ทำได้ โดยนำเวกเตอร์ที่เป็นตัวตั้ง จากนั้นเอาหางของเวกเตอร์ที่เป็นผลบวกหรือผลต่าง มาต่อกับหัวของเวกเตอร์ตัวตั้ง
โดยเขียนให้ถูกต้องทั้งขนาดและทิศทาง เวกเตอร์ลัพธ์หาได้จาก หางเวกเตอร์แรก ไปยังหัวเวกเตอร์สุดท้าย

จากรูป ใช้กฏของโคไซน์ ( Cosine's Law ) จะได้ว่า  =
= 
2) วิธีการทางคณิตศาสตร์ ( วิธีการสร้างสี่เหลี่ยมด้านขนาน )
ถ้ามีเวกเตอร์ย่อย 2 อัน สามารถนำมารวมได้โดยแทนขนาดและทิศทาง ด้วยด้านทั้งสองของสี่เหลี่ยมด้านขนาน
ที่ประกอบมุมในจุดนั้น เส้นทแยงมุมที่ลากจากจุดนั้นไปยังมุมตรงข้ามจะแทนทั้งขนาด และทิศทางของเวกเตอร์ลัพธ์

การหาขนาดของเวกเตอร์ลัพธ์หาได้จาก 
ส่วนการลบเวกเตอร์ให้ทำคล้าย ๆ กันกับการบวกเวกเตอร์เพียงแต่ให้กลับทิศทางของเวกเตอร์ตัวลบ
ปริมาณเวกเตอร์
ปริมาณกายภาพแบ่งออกได้ 2 ประเภท
1. ปริมาณสเกล่าร์ คือปริมาณที่บอกแต่ขนาดอย่างเดียวก็ได้ความหมายสมบูรณ์ ไม่ต้องบอกทิศทาง เช่น ระยะทาง มวล เวลา ปริมาตร ความหนาแน่น งาน พลังงาน ฯลฯ
การหาผลลัพธ์ของปริมาณสเกล่าร์ ก็อาศัยหลังการทางพีชคณิต คือ วิธีการ บวก ลบ คูณ หาร
2. ปริมาณเวกเตอร์ คือ ปริมาณที่ต้องบอกทั้งขนาดและทิศทาง จึงจะได้ความหมายสมบูรณ์ เช่น การกระจัด ความเร่ง ความเร็ว แรง โมเมนตัม ฯลฯ
การหาผลลัพธ์ของปริมาณเวกเตอร์ ต้องอาศัยวิธีการทางเวคเตอร์ โดยต้องหาผลลัพธ์ทั้งขนาดและทิศทาง
การหาผลลัพธ์ของปริมาณสเกล่าร์ ก็อาศัยหลังการทางพีชคณิต คือ วิธีการ บวก ลบ คูณ หาร
2. ปริมาณเวกเตอร์ คือ ปริมาณที่ต้องบอกทั้งขนาดและทิศทาง จึงจะได้ความหมายสมบูรณ์ เช่น การกระจัด ความเร่ง ความเร็ว แรง โมเมนตัม ฯลฯ
การหาผลลัพธ์ของปริมาณเวกเตอร์ ต้องอาศัยวิธีการทางเวคเตอร์ โดยต้องหาผลลัพธ์ทั้งขนาดและทิศทาง
1. สัญลักษณ์ของปริมาณเวกเตอร์
ใช้อักษรมีลูกศรครึ่งบนชี้จากซ้ายไปขวา หรือใช้ตัวอักษรทึบแสดงปริมาณเวกเตอร์ก็ได้
2. เวกเตอร์ที่เท่ากัน
เวกเตอร์ 2 เวกเตอร์เท่ากัน เมื่อเวกเตอร์ทั้งสองเท่ากันและมีทิศไปทางเดียวกัน
3. เวกเตอร์ลัพธ์ใช้อักษร R
4. การบวก-ลบเวกเตอร์
การบวก-ลบเวกเตอร์ หรือการหาเวกเตอร์ สามารถทำได้ 2 วิธี คือ
1. วิธีการเขียนรูป
2. วิธีการคำนวณ
1.1 การหาเวกเตอร์ลัพธ์โดยวิธีการเขียนรูปแบบหางต่อหัว มีขั้นตอนดังนี้
(1) เขียนลูกศรตามเวกเตอร์แรกตามขนาดและทิศทางที่กำหนด
(2) นำหางลูกศรของเวกเตอร์ที่ 2 ที่โจทย์กำหนด ต่อหัวลูกศรของเวกเตอร์แรก
(3) นำหางลูกศรของเวกเตอร์ที่ 3 ที่โจทย์กำหนด ต่อหัวลูกศรของเวกเตอร์ที่ 2
(4) ถ้ามีเวกเตอร์ย่อยๆอีก ให้นำเวกเตอร์ต่อๆไป มากระทำดังข้อ (3) จนครบทุกเวกเตอร์
(5) เวกเตอร์ลัพธ์หาได้โดยการลากลูกศรจากหางของเวกเตอร์แรกไปยังหัวของเวกเตอร์สุดท้าย เช่น


นิยามต้องทราบ
ถ้า A เป็นเวกเตอร์ใดๆที่มีขนาดและทิศทางหนึ่งๆ เวกเตอร์ -A คือ เวกเตอร์ที่มีขนาดเท่ากับเวกเตอร์ A แต่ มี ทิศทางตรงกันข้าม
1.2 การหาเวกเตอร์ลัพธ์โดยวิธีการคำนวณ
เนื่องจากการหาเวกเตอร์ลัพธ์โดยวิธีการวาดรูป ให้ผลลัพธ์ไม่แม่นยำเพียงแต่ได้คร่าวๆ เท่านั้น เพราะถ้าลากความยาวหรือทิศทางลูกศรแทนเวกเตอร์คลาดเคลื่อนเพียงเล็กน้อย ผลของเวกเตอร์ลัพธ์ก็จะคลาดเคลื่อนไปด้วยแต่การหาเวกเตอร์ลัพธ์โดยการคำนวณจะให้ผลลัพธ์ถูกต้องแน่นอน
การหาเวกเตอร์ลัพธ์โดยวิธีการคำนวณ เมื่อมีเวกเตอร์ย่อยเพียง 2 เวกเตอร์ จะแบ่งออกเป็น 3 ลักษณะ ดังนี้
1. เวกเตอร์ทั้ง 2 ไปทางเดียวกัน เวกเตอร์ลัพธ์มีขนาดเท่ากับผลบวกของขนาดเวกเตอร์ทั้งสอง ทิศทางของเวกเตอร์ไปทางเดียวกับเวกเตอร์ทั้งสอง
2. เวกเตอร์ทั้ง 2 สวนทางกัน เวกเตอร์ลัพธ์มีขนาดเท่ากับผลต่างของเวกเตอร์ทั้งสอง ทิศทางของเวกเตอร์ลัพธ์ไปทางเดียวกับเวกเตอร์ที่มีขนาดมากกว่า
เพราะฉะนั้น R = B - A เมื่อ B > A , R = A - B เมื่อ A > B
3. เวกเตอร์ทั้ง 2 ทำมุม0 ต่อกัน สามารถหาเวกเตอร์ลัพธ์โดยวิธีการเขียนรูปสี่เหลี่ยมด้านขนาน โดยให้เวกเตอร์ย่อยเป็นด้านของสี่เหลี่ยมด้านขนานที่ประกอบ ณ จุดนั้น จะ ได้เวกเตอร์ลัพธ์มีขนาดและทิศทางตามแนวเส้นทแยงมุมของสี่เหลี่ยมด้านขนานที่ลากจากจุดที่เวกเตอร์ทั้งสองกระทำต่อกัน
ระยะทาง (Distance) คือ ความยาววัดตามแนวเส้นที่อนุภาคเคลื่อนที่ เป็นปริมาณสเกล่าร์(มีเฉพาะขนาด)หน่วยมาตรฐาน SI คือ "เมตร"
การขจัด หรือ การกระจัด (Displacement) คือ เส้นตรงที่ลากจากจุดตั้งต้นของการเคลื่อนที่ไปยังจุดสุดท้ายของการเคลื่อนที่ เป็นปริมาณเวกเตอร์ มีทั้งขนาดและทิศทาง (คือ ทิศจากที่หัวศรลากจากจุดตั้งต้นไปสุดท้าย)มีหน่วย "เมตร" เช่นกัน
ถ้า A เป็นเวกเตอร์ใดๆที่มีขนาดและทิศทางหนึ่งๆ เวกเตอร์ -A คือ เวกเตอร์ที่มีขนาดเท่ากับเวกเตอร์ A แต่ มี ทิศทางตรงกันข้าม
1.2 การหาเวกเตอร์ลัพธ์โดยวิธีการคำนวณ
เนื่องจากการหาเวกเตอร์ลัพธ์โดยวิธีการวาดรูป ให้ผลลัพธ์ไม่แม่นยำเพียงแต่ได้คร่าวๆ เท่านั้น เพราะถ้าลากความยาวหรือทิศทางลูกศรแทนเวกเตอร์คลาดเคลื่อนเพียงเล็กน้อย ผลของเวกเตอร์ลัพธ์ก็จะคลาดเคลื่อนไปด้วยแต่การหาเวกเตอร์ลัพธ์โดยการคำนวณจะให้ผลลัพธ์ถูกต้องแน่นอน
การหาเวกเตอร์ลัพธ์โดยวิธีการคำนวณ เมื่อมีเวกเตอร์ย่อยเพียง 2 เวกเตอร์ จะแบ่งออกเป็น 3 ลักษณะ ดังนี้
1. เวกเตอร์ทั้ง 2 ไปทางเดียวกัน เวกเตอร์ลัพธ์มีขนาดเท่ากับผลบวกของขนาดเวกเตอร์ทั้งสอง ทิศทางของเวกเตอร์ไปทางเดียวกับเวกเตอร์ทั้งสอง
2. เวกเตอร์ทั้ง 2 สวนทางกัน เวกเตอร์ลัพธ์มีขนาดเท่ากับผลต่างของเวกเตอร์ทั้งสอง ทิศทางของเวกเตอร์ลัพธ์ไปทางเดียวกับเวกเตอร์ที่มีขนาดมากกว่า
เพราะฉะนั้น R = B - A เมื่อ B > A , R = A - B เมื่อ A > B
3. เวกเตอร์ทั้ง 2 ทำมุม
ระยะทาง (Distance) คือ ความยาววัดตามแนวเส้นที่อนุภาคเคลื่อนที่ เป็นปริมาณสเกล่าร์(มีเฉพาะขนาด)หน่วยมาตรฐาน SI คือ "เมตร"
การขจัด หรือ การกระจัด (Displacement) คือ เส้นตรงที่ลากจากจุดตั้งต้นของการเคลื่อนที่ไปยังจุดสุดท้ายของการเคลื่อนที่ เป็นปริมาณเวกเตอร์ มีทั้งขนาดและทิศทาง (คือ ทิศจากที่หัวศรลากจากจุดตั้งต้นไปสุดท้าย)มีหน่วย "เมตร" เช่นกัน
การเคลื่อนที่ของวัตถุ
ปริมาณที่เกี่ยวข้องกับการเคลื่อนที่จะเป็นพื้นฐานในการศึกษาเรื่องของการเคลื่อนที่ ซึ่งในการเคลื่อนที่จะต้องประกอบไปด้วยองค์ประกอบ 3 ส่วน
Y วัตถุที่เคลื่อนที่ จะหมายจึงวัตถุที่มีลักษณะเป็นของแข็งที่คงรูปทรงอยู่ได้
Y ผู้สังเกต เป็นผู้ที่ศึกษาวัตถุที่เคลื่อนที่ โดยผู้สังเกตจะต้องอยู่นอกวัตถุที่เคลื่อนที่
Y จุดอ้างอิง การเคลื่อนที่ของวัตถุจะต้องมีการเปลี่ยนตำแหน่งของวัตถุดังนั้นเราจะต้องมีจุดอ้างอิง
เพื่อบอกตำแหน่งของวัตถุเมื่อเวลาผ่านไป
1. ระยะทาง (Distance) การเคลื่อนที่ของวัตถุจะเริ่มนับตั้งแต่จุดเริ่มต้นที่เราสังเกตเป็นจุดอ้างอิงแล้ววัดระยะทางตามแนวทางที่วัตถุเคลื่อนที่
ไปตามแนวทางการเคลื่อนที่ของวัตถุ
เพื่อบอกตำแหน่งของวัตถุเมื่อเวลาผ่านไป
1. ระยะทาง (Distance) การเคลื่อนที่ของวัตถุจะเริ่มนับตั้งแต่จุดเริ่มต้นที่เราสังเกตเป็นจุดอ้างอิงแล้ววัดระยะทางตามแนวทางที่วัตถุเคลื่อนที่
ไปตามแนวทางการเคลื่อนที่ของวัตถุ
2. การกระจัด (Displacement) เป็นการบอกตำแหน่งของวัตถุหลังจากการที่เคลื่อนที่ไปแล้วในช่วงเวลาหนึ่งโดยจะบอกว่าห่างจากจุดเริ่มต้นเป็นระยะ
เท่าไร และอยู่ทางทิศไหนของจุดเริ่มต้น ดังนั้นการกระจัดเป็น ปริมาณเวกเตอร์ เพราะมีทั้งขนาดและทิศทาง
*********ถ้าวัตถุเคลื่อนที่กลับมาสู่จุดเริ่มต้น การกระจัดจะมีค่าเป็นศูนย์**********
เท่าไร และอยู่ทางทิศไหนของจุดเริ่มต้น ดังนั้นการกระจัดเป็น ปริมาณเวกเตอร์ เพราะมีทั้งขนาดและทิศทาง
*********ถ้าวัตถุเคลื่อนที่กลับมาสู่จุดเริ่มต้น การกระจัดจะมีค่าเป็นศูนย์**********
3. เวลา (Time) การวัดเวลาเรานับ ณ จุดเริ่มสังเกต ซึ่งขณะนั้นวัตถุอาจจะหยุดนิ่ง หรือเคลื่อนที่อยู่ก็ตาม ค่าของเวลาจะมีความสัมพันธ์กับระยะทาง เมื่อเวลาผ่านไป ระยะทางที่วัตถุเคลื่อนที่ก็จะเพิ่มขึ้น ในบางครั้งอาจจะมีข้อมูลของระยะทางกับเวลาสัมพันธ์กัน
4. อัตราเร็ว (Speed) หมายถึง ระยะทางที่วัตถุเคลื่อนที่ได้ในหนึ่งหน่วยเวลา เป็นปริมาณสเกลาร์ มีหน่วยเป็น เมตร/วินาที
V แทน อัตราเร็ว มีหน่วยเป็น เมตร/วินาที (m/s)
S แทน ระยะทาง มีหน่วยเป็น เมตร (m)
t แทน เวลา มีหน่วยเป็น วินาที (s )
5. ความเร็ว (Velocity) หมายถึง การกระจัดของวัตถุที่เปลี่ยนไปในหน่วยเวลา
t แทน เวลา มีหน่วยเป็น วินาที (s )
6. ความเร่ง (Acceleration) ความเร็วที่เปลี่ยนไปในหนึ่งหน่วยเวลา
 ลักษณะของการเคลื่อนที่ลักษณะของการเคลื่อนที่แบ่งได้ 4 ลักษณะ คือ
ลักษณะของการเคลื่อนที่ลักษณะของการเคลื่อนที่แบ่งได้ 4 ลักษณะ คือ
1. การเคลื่อนที่เป็นแนวเส้นตรง
ลักษณะของการเคลื่อนที่แบบนี้เป็นพื้นฐานของการเคลื่อนที่ เพราะทิศทางการเคลื่อนที่จะมีทิศทางเดียว
แต่อาจจะเคลื่อนที่ไป-กลับได้ รูปแบบการเคลื่อนที่อาจจะแตกต่างกันออกไป ตัวอย่างเช่น
ลักษณะของการเคลื่อนที่แบบนี้เป็นพื้นฐานของการเคลื่อนที่ เพราะทิศทางการเคลื่อนที่จะมีทิศทางเดียว
แต่อาจจะเคลื่อนที่ไป-กลับได้ รูปแบบการเคลื่อนที่อาจจะแตกต่างกันออกไป ตัวอย่างเช่น
- การเคลื่อนที่ของรถไฟบนราง
- การเคลื่อนที่ของรถบนถนนที่เป็นแนวเส้นตรง
- การเคลื่อนที่ภายใต้แรงโน้มถ่วงของโลก
2. การเคลื่อนที่แบบโพรเจกไทล์
เป็นการเคลื่อนที่ของวัตถุที่มีแนวเส้นทางการเคลื่อนที่เป็นรูปโค้งพาราโบลา และเป็นพาราโบลาทางแกน y
ที่มีลักษณะคว่ำการที่วัตถุเคลื่อนที่เป็นแนวเส้นโค้งเนื่องจากวัตถุเคลื่อนที่เข้าไปในบริเวณที่มีแรงกระทำต่อ
วัตถุไม่อยู่ในแนวเดียวกับทิศของการเคลื่อนที่
เป็นการเคลื่อนที่ของวัตถุที่มีแนวเส้นทางการเคลื่อนที่เป็นรูปโค้งพาราโบลา และเป็นพาราโบลาทางแกน y
ที่มีลักษณะคว่ำการที่วัตถุเคลื่อนที่เป็นแนวเส้นโค้งเนื่องจากวัตถุเคลื่อนที่เข้าไปในบริเวณที่มีแรงกระทำต่อ
วัตถุไม่อยู่ในแนวเดียวกับทิศของการเคลื่อนที่
3. การเคลื่อนที่แบบวงกลม
เป็นการเคลื่อนที่ของวัตถุรอบจุดๆหนึ่ง โดยมีรัศมีคงที่ การเคลื่อนที่เป็นวงกลม
ทิศทางของการเคลื่อนที่จะเปลี่ยนแปลงตลอดเวลา ความเร็วของวัตถุจะเปลี่ยนไปตลอดเวลา ทิศของแรงที่กระทำจะตั้งฉากกับทิศของการเคลื่อนที่
แรงที่กระทำต่อวัตถุจะมีทิศทางเข้าสู่ศูนย์กลาง เราจึงเรียกว่า “แรงสู่ศูนย์กลาง”
ในขณะเดียวกัน จะมีแรงต้านที่ไม่ให้วัตถุเข้าสู่ศูนย์กลาง เราเรียกว่า “แรงหนีศูนย์กลาง” แรงหนีศูนย์กลางจะเท่ากับแรงสู่ศูนย์กลาง วัตถุจึงจะเคลื่อนที่เป็นวงกลมได้
เป็นการเคลื่อนที่ของวัตถุรอบจุดๆหนึ่ง โดยมีรัศมีคงที่ การเคลื่อนที่เป็นวงกลม
ทิศทางของการเคลื่อนที่จะเปลี่ยนแปลงตลอดเวลา ความเร็วของวัตถุจะเปลี่ยนไปตลอดเวลา ทิศของแรงที่กระทำจะตั้งฉากกับทิศของการเคลื่อนที่
แรงที่กระทำต่อวัตถุจะมีทิศทางเข้าสู่ศูนย์กลาง เราจึงเรียกว่า “แรงสู่ศูนย์กลาง”
ในขณะเดียวกัน จะมีแรงต้านที่ไม่ให้วัตถุเข้าสู่ศูนย์กลาง เราเรียกว่า “แรงหนีศูนย์กลาง” แรงหนีศูนย์กลางจะเท่ากับแรงสู่ศูนย์กลาง วัตถุจึงจะเคลื่อนที่เป็นวงกลมได้
4. การเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย
ลักษณะของการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย จะเป็นการเคลื่อนที่ที่มีลักษณะ
พิเศษ คือ วัตถุจะเคลื่อนที่กลับไปกลับมาที่เราเรียกว่า แกว่ง หรือ สั่น การเคลื่อนที่แบบนี้จะเป็นการเคลื่อนที่อยู่ในช่วงสั้นๆ มีขอบเขตจำกัด เราเรียกว่า แอมพลิจูด (Amplitude) โดยนับจากตำแหน่งสมดุล ซึ่งอยู่ตรงจุดกลางวัดไปทางซ้ายหรือขวา เช่น การแกว่งของชิงช้า หรือยานไวกิงในสวนสนุก
ลักษณะของการเคลื่อนที่แบบฮาร์มอนิกอย่างง่าย จะเป็นการเคลื่อนที่ที่มีลักษณะ
พิเศษ คือ วัตถุจะเคลื่อนที่กลับไปกลับมาที่เราเรียกว่า แกว่ง หรือ สั่น การเคลื่อนที่แบบนี้จะเป็นการเคลื่อนที่อยู่ในช่วงสั้นๆ มีขอบเขตจำกัด เราเรียกว่า แอมพลิจูด (Amplitude) โดยนับจากตำแหน่งสมดุล ซึ่งอยู่ตรงจุดกลางวัดไปทางซ้ายหรือขวา เช่น การแกว่งของชิงช้า หรือยานไวกิงในสวนสนุก
รูป การสั่นและแกว่งของวัตถุ

ระยะทาง
ในขณะที่เราเคลื่อนที่ เราจะเปลี่ยนตำแหน่งที่อยู่ตลอดแนว

ระยะทาง (distance) คือ ความยาว
การกระจัด (displacement) คือ เส้นตรง
ตัวอย่างที่ 1


ชายคนหนึ่งเดินจาก ก ไป ข แล้วจาก ข ไป ค และไป ง
ชายคนนี้จะได้ระยะทาง = 6 + 3 + 2 เมตร = 11 เมตร
ชายคนนี้จะได้การกระจัด = 5 เมตร
ตัวอย่างที่ 2


ถ้าวัตถุเคลื่อนที่ จาก A ไป B ตามเส้นทาง S1 จะได้ระยะทาง = S1, ระยะกระจัด = S3
ถ้าวัตถุเคลื่อนที่ จาก A ไป B ตามเส้นทาง S2 จะได้ระยะทาง = S2, ระยะกระจัด = S3
ถ้าวัตถุเคลื่อนที่ จาก A ไป B ตามเส้นทาง S3 จะได้ระยะทาง = S3, ระยะกระจัด = S3
ถ้าวัตถุเคลื่อนที่ จาก A ไป B ตามเส้นทาง S4 จะได้ระยะทาง = S4, ระยะกระจัด = S3
การกระจัดจึงมีค่าเท่ากับระยะทาง เมื่อวัตถุเคลื่อนที่เป็นเส้นตรง
การกระจัด
การกระจัด หรือ การขจัด คือระยะทางที่สั้นที่สุดจากจุดเริ่มต้นไปยังจุดสิ้นสุด [1] ระยะทางที่สั้นที่สุดก็คือความยาวของเส้นตรงสมมติที่ลากจากจุดเริ่มต้นไปยังจุดสิ้นสุด ดังนั้นมันจึงอาจแตกต่างจากเส้นทางเดินปกติก็ได้ เวกเตอร์การกระจัด ก็คือความยาวและทิศทางของเส้นตรงสมมติดังกล่าว
เวกเตอร์ตำแหน่งเป็นตัวบ่งชี้ตำแหน่งของจุด P ในปริภูมิ ซึ่งเกี่ยวข้องกับการกระจัดจากจุดอ้างอิง O (โดยทั่วไปจะเป็นจุดกำเนิดของระบบพิกัด) เวกเตอร์ตำแหน่งแสดงให้เห็นว่า ถ้าเคลื่อนที่ไปในแนวเส้นตรงโดยเริ่มจากจุด O ด้วยระยะทางและทิศทางนั้น ก็จะพบกับจุด P ที่ปลายทาง
การกระจัดอาจถูกเรียกว่าเป็น เวกเตอร์ตำแหน่งสัมพัทธ์ กล่าวคือ เมื่อเวกเตอร์ตำแหน่งสิ้นสุด Rf สัมพันธ์กับเวกเตอร์ตำแหน่งเริ่มต้น Ri เวกเตอร์การกระจัดสามารถนิยามขึ้นได้จากผลต่างระหว่างเวกเตอร์สิ้นสุดกับเวกเตอร์เริ่มต้น ดังนี้ (สัญกรณ์ตัวหนาหมายถึงเวกเตอร์)
-
- อัตราเร็ว

- เมตรต่อวินาที, (สัญลักษณ์ m/s) , ระบบหน่วย SI
- กิโลเมตรต่อชั่วโมง, (สัญลักษณ์ km/h)
- ไมล์ต่อชั่วโมง, (สัญลักษณ์ mph)
- นอต (ไมล์ทะเลต่อชั่วโมง, สัญลักษณ์ kt)
- มัค เมื่อมัค 1 เท่ากับ อัตราเร็วเสียง มัค n เท่ากับ n เท่าของอัตราเร็วเสียง
-
- มัค 1 ≈ 343 m/s ≈ 1235 km/h ≈ 768 mi/h (ดู อัตราเร็วเสียง สำหรับข้อมูลเพิ่มเติม)
- อัตราเร็วแสง ใน สุญญากาศ (สัญลักษณ์ c) เป็นหนึ่งใน หน่วยธรรมชาติ
-
- c = 299,792,458 m/s
- การเปลี่ยนหน่วยที่สำคัญ
-
- 1 m/s = 3.6 km/h
- 1 mph = 1.609 km/h
- 1 knot = 1.852 km/h = 0.514 m/s





- สำหรับมนุษย์ อัตราเร็วของ การเดิน ของมนุษย์อยู่ที่ประมาณ (~5 km/h, 1.39 m/s) ถึงแม้ว่ามันจะขึ้นอยู่กับปัจจัยหลายอย่าง เช่น ความสูง น้ำหนัก และอายุ
- การวิ่ง: อัตราเร็วสำหรับระยะทางไกล การจ้อกกิ้ง สำหรับคนโดยเฉลี่ยอยู่ที่ประมาณ 6 mph (~10 km/h, 2.7 m/s) นักกีฬาชั้นยอดสามารถวิ่งเต็มเหยียดด้วยอัตราเร็ว 23.03 mph (~36.85 km/h, 10.24 m/s) ภายในระยะทางสั้น ๆ เช่น การวิ่ง 200 เมตร
- การขี่จักรยาน: 12 mph (~20 km/h, 5.56 m/s)
- รถยนต์: โดยเฉลี่ย 65 mph (~104 km/h, 28.9 m/s ) บนทางด่วน
-
- ดูบทความหลักที่ สมการการเคลื่อนที่
-
-
-
-
-

- อัตราเร่ง
- กรณีที่วัตถุเคลื่อนที่อัตราเร็วที่ไม่สม่ำเสมอ หรือความเร็วไม่สม่ำเสมอ วัตถุมีค่าความเร่งความหมายของอัตราเร่งหรือความเร่ง คือ อัตราเร็วหรือ ความเร็วที่เปลี่ยนไปในหนึ่งหน่วยเวลาที่วัตถุมีการเคลื่อนที่การคำนวณหาค่าอัตราเร่ง ทำได้โดยหาอัตราเร็วที่เปลี่ยนไปโดยใช้อัตราเร็วสุดท้ายของการเคลื่อนที่ลบด้วยอัตราเร็วเริ่มต้นของการเคลื่อนที่ หารด้วยเวลาที่ใช้เปลี่ยนค่าอัตราเร็วนั้น เช่นความเร่งในฟิสิกส์ ความเร่ง (อังกฤษ: acceleration, สัญลักษณ์: a) คือ อัตราการเปลี่ยนแปลง (หรืออนุพันธ์เวลา) ของความเร็ว เป็นปริมาณเวกเตอร์ที่มีหน่วยเป็น ความยาว/เวลา² ในหน่วยเอสไอกำหนดให้หน่วยเป็น เมตร/วินาที²เมื่อวัตถุมีความเร่งในช่วงเวลาหนึ่ง ความเร็วของมันจะเปลี่ยนแปลงไป ความเร่งอาจมีค่าเป็นบวกหรือลบก็ได้ ซึ่งเรามักว่าเรียกความเร่ง กับ ความหน่วง ตามลำดับ ความเร่งมีนิยามว่า "อัตราการเปลี่ยนแปลงความเร็วของวัตถุในช่วงเวลาหนึ่ง" และกำหนดโดยสมการนี้เมื่อ
- a คือ เวกเตอร์ความเร่ง
- v คือ เวกเตอร์ความเร็ว ในหน่วย m/s
- t คือ เวลา ในหน่วยวินาที
จากสมการนี้ a จะมีหน่วยเป็น m/s² (อ่านว่า "เมตรต่อวินาทียกกำลังสอง")หรือเขียนเป็นอีกสมการได้เมื่อ คือ ความเร่งเฉลี่ย (m/s²)
คือ ความเร่งเฉลี่ย (m/s²)
 คือ ความเร็วต้น (m/s)
คือ ความเร็วต้น (m/s)
 คือ ความเร็วปลาย (m/s)
คือ ความเร็วปลาย (m/s)
 คือ ช่วงเวลา (s)
คือ ช่วงเวลา (s)
อัตราเร็ว (สัญลักษณ์: v) คืออัตราของ การเคลื่อนที่ หรือ อัตราการเปลี่ยนแปลงของตำแหน่งก็ได้ หลายครั้งมักเขียนในรูป ระยะทาง d ที่เคลื่อนที่ไปต่อ หน่วย ของ เวลา tอัตราเร็ว เป็นปริมาณสเกลาร์ที่มีมิติเป็นระยะทาง/เวลา ปริมาณเวกเตอร์ที่เทียบเท่ากับอัตราเร็วคือความเร็ว อัตราเร็ววัดในหน่วยเชิงกายภาพเดียวกับความเร็ว แต่อัตราเร็วไม่มีองค์ประกอบของทิศทางแบบที่ความเร็วมี อัตราเร็วจึงเป็นองค์ประกอบส่วนที่เป็นขนาดของความเร็วในรูปสัญลักษณ์ทางคณิตศาสตร์ อัตราเร็วคือหน่วยของอัตราเร็ว ได้แก่ยานพาหนะต่าง ๆ มักมี speedometer สำหรับวัดอัตราเร็ววัตถุที่เคลื่อนที่ไปตามแนวราบ พร้อม ๆ กับแนวดิ่ง (เช่น อากาศยาน) จะแยกประเภทเป็น forward speed กับ climbing speedเนื้อหา
[ซ่อน][แก้]อัตราเร็วเฉลี่ย
อัตราเร็วในรูป สมบัติเชิงกายภาพ มักแทนอัตราเร็วที่ขณะใดขณะหนึ่ง ในชีวิตจริงเรามันใช้ อัตราเร็วเฉลี่ย (ใช้สัญลักษณ์ ) ซึ่งก็คือ อัตรา ของ ระยะทาง รวม (หรือ ความยาว) ต่อช่วง เวลายกตัวอย่างเช่น ถ้าคุณเคลื่อนที่ได้ 60 ไมล์ในเวลา 2 ชั่วโมง อัตราเร็ว เฉลี่ย ของคุณในช่วงเวลานั้นคือ 60/2 = 30 ไมล์ต่อชั่วโมง แต่อัตราเร็วที่ขณะใดขณหนึ่งย่อมเปลี่ยนแปลงต่างกันไปในรูปสัญลักษณ์ทางคณิตศาสตร์อัตราเร็วที่ขณะใดขณะหนึ่งซึ่งนิยามเป็นฟังก์ชันของ เวลา ในช่วงเวลา
) ซึ่งก็คือ อัตรา ของ ระยะทาง รวม (หรือ ความยาว) ต่อช่วง เวลายกตัวอย่างเช่น ถ้าคุณเคลื่อนที่ได้ 60 ไมล์ในเวลา 2 ชั่วโมง อัตราเร็ว เฉลี่ย ของคุณในช่วงเวลานั้นคือ 60/2 = 30 ไมล์ต่อชั่วโมง แต่อัตราเร็วที่ขณะใดขณหนึ่งย่อมเปลี่ยนแปลงต่างกันไปในรูปสัญลักษณ์ทางคณิตศาสตร์อัตราเร็วที่ขณะใดขณะหนึ่งซึ่งนิยามเป็นฟังก์ชันของ เวลา ในช่วงเวลา![[t_0, t_1]](http://upload.wikimedia.org/wikipedia/th/math/0/b/3/0b3b8cb99d808fe833d8f1c61cac6b2e.png) จะให้อัตราเร็วเฉลี่ยในรูปในขณะที่อัตราเร็วที่ขณะใดขณะหนึ่งซึ่งนิยามเป็นฟังก์ชันของ ระยะทาง (หรือ ความยาว) ในช่วงความยาว
จะให้อัตราเร็วเฉลี่ยในรูปในขณะที่อัตราเร็วที่ขณะใดขณะหนึ่งซึ่งนิยามเป็นฟังก์ชันของ ระยะทาง (หรือ ความยาว) ในช่วงความยาว![[l_0, l_1]](http://upload.wikimedia.org/wikipedia/th/math/8/7/2/8722996cc2ef22ea31fa9b4bd65b734f.png) จะให้อัตราเร็วเฉลี่ยในรูปบ่อยครั้งที่มีคนคาดโดยสัญชาตญาณ แต่ผิด ว่าการเคลื่อนที่ครึ่งแรกของระยะทางด้วยอัตราเร็ว
จะให้อัตราเร็วเฉลี่ยในรูปบ่อยครั้งที่มีคนคาดโดยสัญชาตญาณ แต่ผิด ว่าการเคลื่อนที่ครึ่งแรกของระยะทางด้วยอัตราเร็ว และระยะทางครึ่งที่สองด้วยอัตราเร็ว
และระยะทางครึ่งที่สองด้วยอัตราเร็ว  จะให้อัตราเร็วเฉลี่ยรวมเป็น
จะให้อัตราเร็วเฉลี่ยรวมเป็น  ค่าที่ถูกต้องต้องเป็น
ค่าที่ถูกต้องต้องเป็น 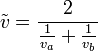
(ระลึกไว้ว่า อย่างแรกเป็น ค่าเฉลี่ยเลขคณิต ในขณะที่อย่างที่สองเป็น ค่าเฉลี่ยฮาร์มอนิก)อัตราเร็วเฉลี่ยสามารถหาได้จาก distribution function ของอัตราเร็วได้เช่นกัน (ทั้งในรูประยะทางหรือเวลาก็ตาม)[แก้]นัยสำคัญทางวัฒนธรรม
อัตราเร็วหรือ ความว่องไวของการเคลื่อนที่มีบทบาทสำคัญในวัฒนธรรมของมนุษย์และสัตว์ (ดู การแข่งความเร็ว) มันเป็นองค์ประกอบของ ความนุ่มนวล ความแม่นยำ และ ความแข็งแกร่ง เช่น ใน การเต้นรำ หรือ ศิลปะการรบ สัตว์ที่เป็นสัญลักษณ์ของอัตราเร็วคือ ม้า (PIE *ek'vos มีที่มาจากคำว่า *ok'u- "ว่องไว") นก โดยเฉพาะนกนักล่าอย่าง เหยี่ยว และแมว คือ lynx (ดู Flos Duellatorum) สัตว์บกที่รวดเร็วที่สุดคือ ชีต้า ซึ่งมีอัตราเร็วในการวิ่งถึง 110 km/h (68 mph) ในระยะทางสั้น ๆ สำหรับอัตราเร็วสม่ำเสมอแล้ว สัตว์บกที่เร็วที่สุดก็คือ ม้าพันธุ์ดีที่ได้รับการฝึก[แก้]อัตราเร็วทั่วไปของวัตถุซึ่งเคลื่อนที่
ความเร็วในทางฟิสิกส์ ความเร็ว คืออัตราการเปลี่ยนแปลงของตำแหน่งต่อหน่วยเวลา มีหน่วยเป็นเมตรต่อวินาที (m/s) ในหน่วยเอสไอ ความเร็วเป็นปริมาณเวกเตอร์ซึ่งประกอบด้วยอัตราเร็วและทิศทาง ขนาดของความเร็วคืออัตราเร็วซึ่งเป็นปริมาณสเกลาร์ ตัวอย่างเช่น "5 เมตรต่อวินาที" เป็นอัตราเร็ว ในขณะที่ "5 เมตรต่อวินาทีไปทางทิศตะวันออก" เป็นความเร็ว ความเร็วเฉลี่ย v ของวัตถุที่เคลื่อนที่ไปด้วยการกระจัดขนาดหนึ่ง ∆x ในช่วงเวลาหนึ่ง ∆t สามารถอธิบายได้ด้วยสูตรนี้อัตราการเปลี่ยนแปลงของความเร็วคือความเร่ง คือการอธิบายว่าอัตราเร็วและทิศทางของวัตถุเปลี่ยนไปอย่างไรในช่วงเวลาหนึ่ง และเปลี่ยนไปอย่างไร ณ เวลาหนึ่ง[แก้]สมการการเคลื่อนที่
เวกเตอร์ความเร็วขณะหนึ่ง v ของวัตถุที่มีตำแหน่ง x (t) ณ เวลา t และตำแหน่ง x (t + ∆t) ณ เวลา t + ∆t สามารถคำนวณได้จากอนุพันธ์ของตำแหน่งสมการของความเร็วของวัตถุยังสามารถหาได้จากปริพันธ์ของสมการของความเร่ง ที่วัตถุเคลื่อนที่ตั้งแต่เวลา t0 ไปยังเวลา tnวัตถุที่มีความเร็วเริ่มต้นเป็น u มีความเร็วสุดท้ายเป็น v และมีความเร่งคงตัว a ในช่วงเวลาหนึ่ง ∆t ความเร็วสุดท้ายหาได้จากความเร็วเฉลี่ยอันเกิดจากความความเร่งคงตัวจึงเป็น ตำแหน่ง x ที่เปลี่ยนไปของวัตถุดังกล่าวในช่วงเวลานั้นหาได้จากกรณีที่ทราบเพียงความเร็วเริ่มต้นของวัตถุเพียงอย่างเดียว คำนวณได้ดังนี้และเมื่อต้องการหาตำแหน่ง ณ เวลา t ใด ๆ ก็สามารถขยายนิพจน์ได้ดังนี้
ตำแหน่ง x ที่เปลี่ยนไปของวัตถุดังกล่าวในช่วงเวลานั้นหาได้จากกรณีที่ทราบเพียงความเร็วเริ่มต้นของวัตถุเพียงอย่างเดียว คำนวณได้ดังนี้และเมื่อต้องการหาตำแหน่ง ณ เวลา t ใด ๆ ก็สามารถขยายนิพจน์ได้ดังนี้






